Riešenie systému rovníc v programe Microsoft Excel

Schopnosť riešiť systémy rovníc môže byť často prínosom nielen pre učenie, ale aj pre prax. Súčasne nie každý používateľ počítača vie, že existujú vlastné varianty riešenia lineárnych rovníc v programe Excel. Dozvieme sa, ako túto úlohu plniť rôznymi nástrojmi tohto stolového procesora rôznymi spôsobmi.

možnosti riešenia

Každá rovnica môže byť považovaná za vyriešená len vtedy, keď sa nájdu jej korene. V programe Excel existuje niekoľko možností na nájdenie koreňov. Pozrime sa na každú z nich.

Metóda 1: Metóda matice

Najbežnejší spôsob riešenia systému lineárnych rovníc pomocou nástrojov programu Excel je použiť metódu matice. Spočíva v zostavovaní matice koeficientov vyjadrenia a potom pri vytváraní inverznej matice. Pokúsime sa použiť túto metódu na vyriešenie nasledujúceho systému rovníc:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


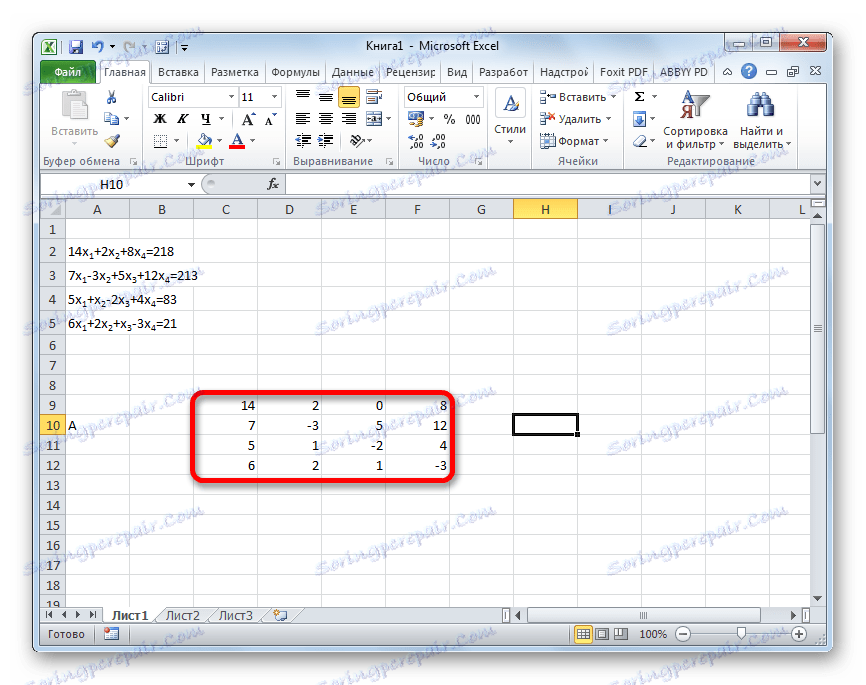
1. Matricu vyplníme číslami, ktoré sú koeficientmi rovnice. Tieto čísla musia byť usporiadané postupne, aby sa zohľadnilo umiestnenie každého koreňa, ku ktorému zodpovedajú. Ak v jednom vyjadrení jeden z koreňov chýba, potom sa v tomto prípade koeficient považuje za rovný nule. Ak koeficient nie je uvedený v rovnici, ale je prítomný zodpovedajúci koreň, predpokladá sa, že koeficient je 1 . Označujeme výslednú tabuľku ako vektor A.
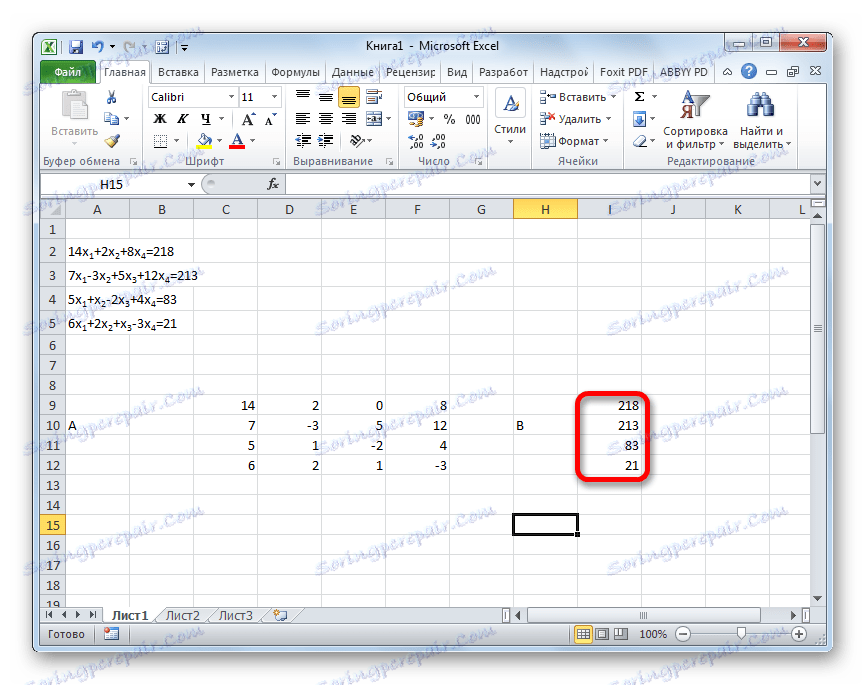
2. Samostatne napíšte hodnoty za znamienkom "sa rovná". Označte ich podľa ich bežného názvu ako vektor B.
3. Najprv nájdeme korene rovnice a musíme nájsť inverznú maticu existujúcej rovnice. Našťastie má spoločnosť Excel špeciálny operátor, ktorý je určený na vyriešenie tohto problému. Nazýva sa to ICBM . Má pomerne jednoduchú syntax:

   =МОБР(массив)

   Argument "Array" je v skutočnosti adresa zdrojovej tabuľky.

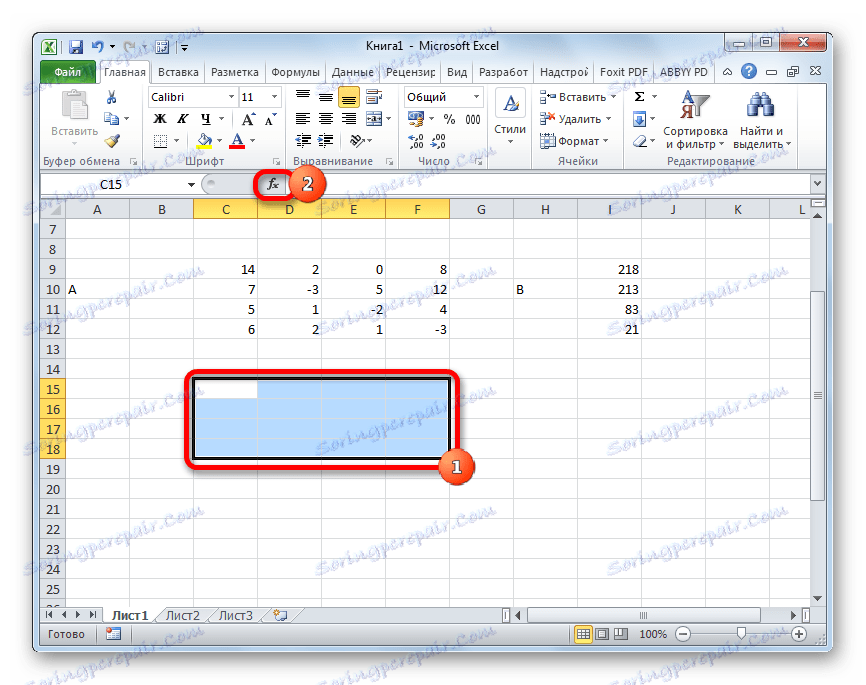
   Takže vyberieme oblasť prázdnych buniek na hárku, ktorá je rovnaká ako veľkosť pôvodnej matice. Klikneme na tlačidlo "Vložiť funkciu" , ktorá sa nachádza v blízkosti riadku vzorca.

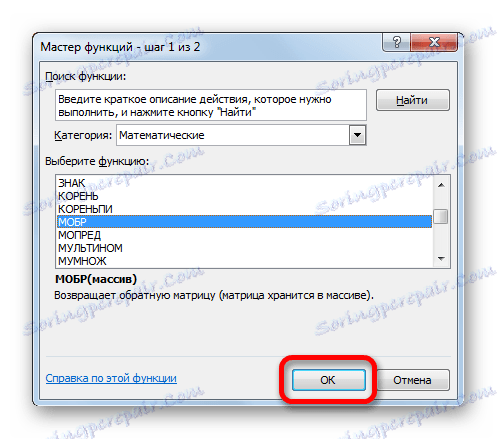
4. Spustí sa Sprievodca funkciami. Pojdme sa do kategórie "Matematické" . V predloženom zozname hľadáme meno "MOBR" . Po jeho nájdení ho vyberte a kliknite na tlačidlo "OK" .
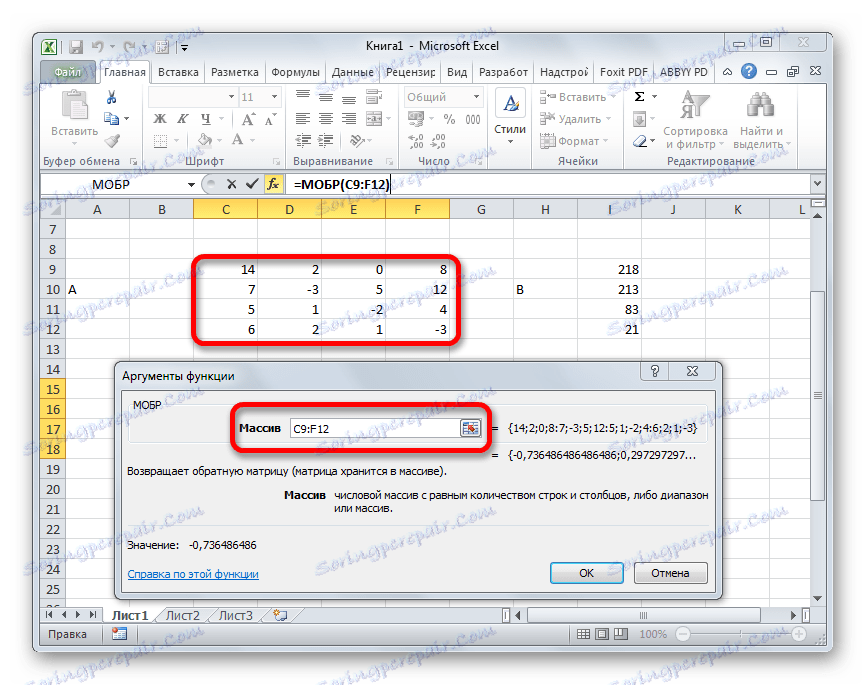
5. Zobrazí sa okno s argumentom funkcie MOBR. Má iba jedno pole v počte argumentov - "Array" . Tu je potrebné zadať adresu našej tabuľky. Na tento účel nastavíme kurzor v tomto poli. Potom držte ľavé tlačidlo myši a vyberte oblasť na hárku, kde je umiestnená matica. Ako vidíte, údaje o súradniciach polohy sa automaticky zadajú do poľa okna. Po dokončení tejto úlohy by bolo najdôležitejšie kliknúť na tlačidlo "OK" , ale neponáhľajte. Faktom je, že kliknutie na toto tlačidlo zodpovedá použitiu príkazu Enter . Ale pri práci s poľa po dokončení vstupu vzorca, nemali by ste kliknúť na tlačidlo Enter , ale urobiť sadu klávesových skratiek Ctrl + Shift + Enter . Túto operáciu vykonávame.
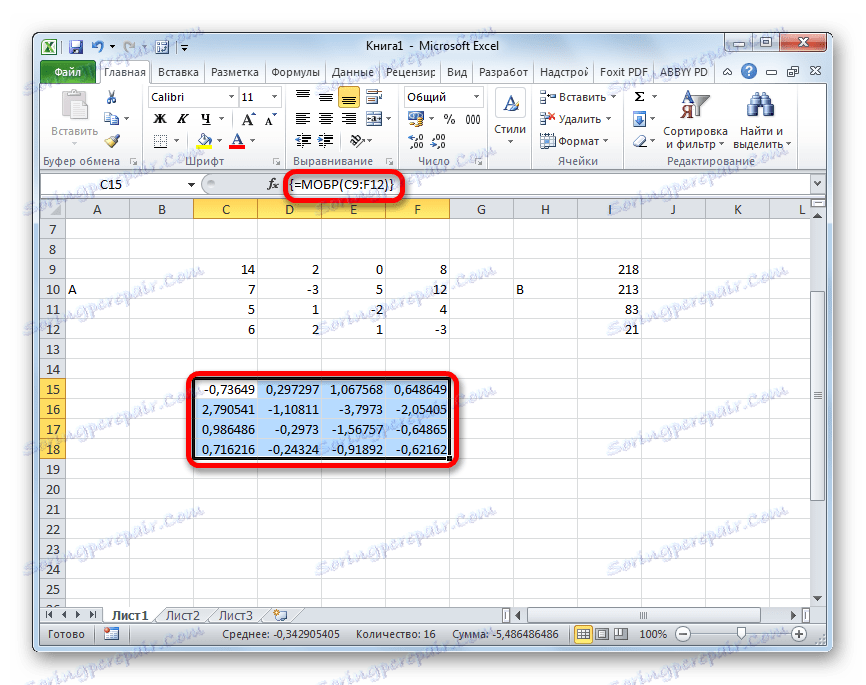
6. Takže potom program vykoná výpočty a na výstupe v predtým pridelenej oblasti máme matricu, ktorá je inverzná k tomuto.
7. Teraz musíme vynásobiť inverznú maticu maticou B , ktorá sa skladá z jedného stĺpca hodnôt umiestnených za znamienkom rovnosti v výrazoch. Pre násobenie tabuliek v programe Excel existuje aj samostatná funkcia, ktorá sa nazýva HUMAN . Toto vyhlásenie má nasledujúcu syntax:

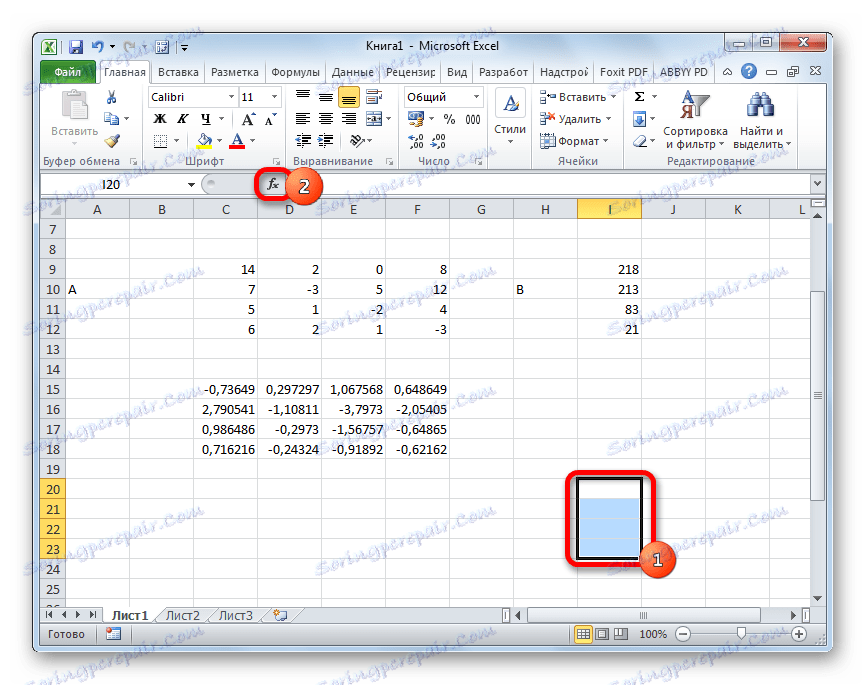
   =МУМНОЖ(Массив1;Массив2)

   Zvolíme rozsah, v našom prípade pozostávajúci zo štyroch buniek. Potom spustíte sprievodcu funkciami kliknutím na ikonu "Vložiť funkciu" .

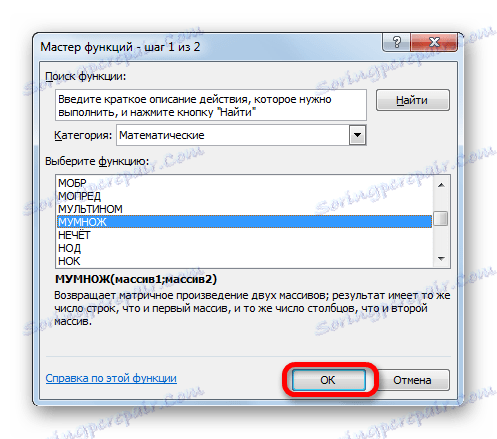
8. V kategórii "Matematická" , Sprievodca začatých funkcií , zvoľte názov "HUMBLE" a kliknite na tlačidlo "OK" .
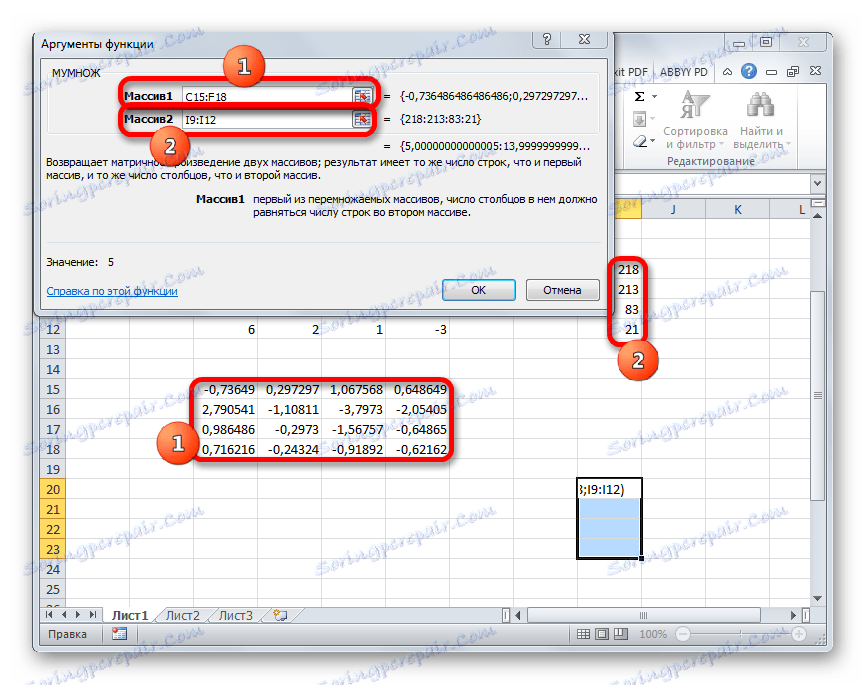
9. Okno argumentov funkcie MULTI . V poli "Array1" zadáme súradnice našej inverznej matice. Preto, rovnako ako v poslednej dobe, nastavíme kurzor v poli a ľavým tlačidlom myši stlačíme príslušnú tabuľku s kurzorom. Vykonávame podobnú akciu na zadanie súradníc do poľa "Array2" , len tentokrát vyberieme hodnoty stĺpca B. Po vykonaní vyššie uvedených krokov znova neponáhľajte stlačiť tlačidlo "OK" alebo kláves Enter a zadajte klávesy Ctrl + Shift + Enter .
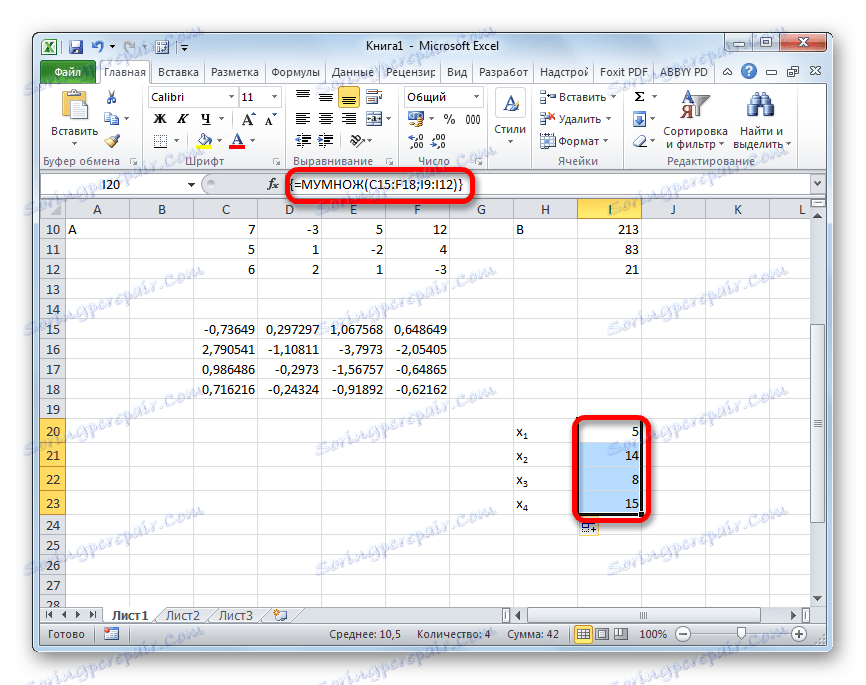
10. Po tejto akcii sa korene rovnice zobrazia v predtým vybranej bunke: X1 , X2 , X3 a X4 . Budú usporiadané postupne. Môžeme teda povedať, že sme tento systém vyriešili. Na overenie správnosti riešenia postačí nahradiť tieto korene pôvodným systémom vyjadrení. Ak je pozorovaná rovnosť, znamená to, že prezentovaný systém rovníc je správne vyriešený.

Lekcia: Inverzná matica v programe Excel

Metóda 2: výber parametrov

Druhá známa metóda riešenia systému rovníc v programe Excel je použitie metódy výberu parametrov. Podstata tejto metódy spočíva v hľadaní opaku. To znamená, že na základe známeho výsledku hľadáme neznámy argument. Použme kvadratickú rovnicu

3x^2+4x-132=0

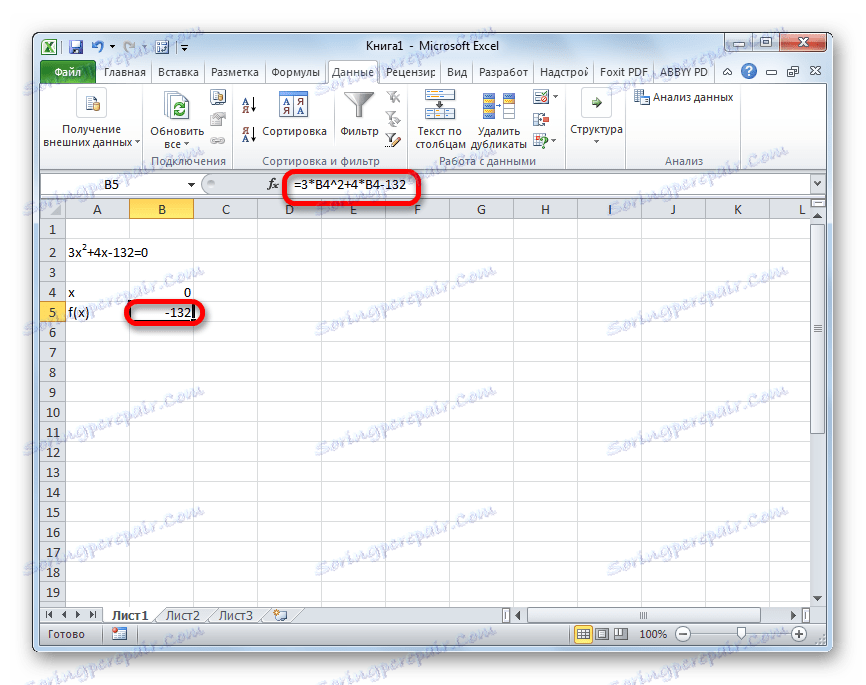
1. Predpokladajme, že hodnota x sa rovná 0 . Vypočítame zodpovedajúcu hodnotu f (x) použitím nasledujúceho vzorca:

   =3*x^2+4*x-132

   Namiesto hodnoty "X" nahraďte adresu bunky, kde sa nachádza číslo 0 , ktoré sme použili pre x .

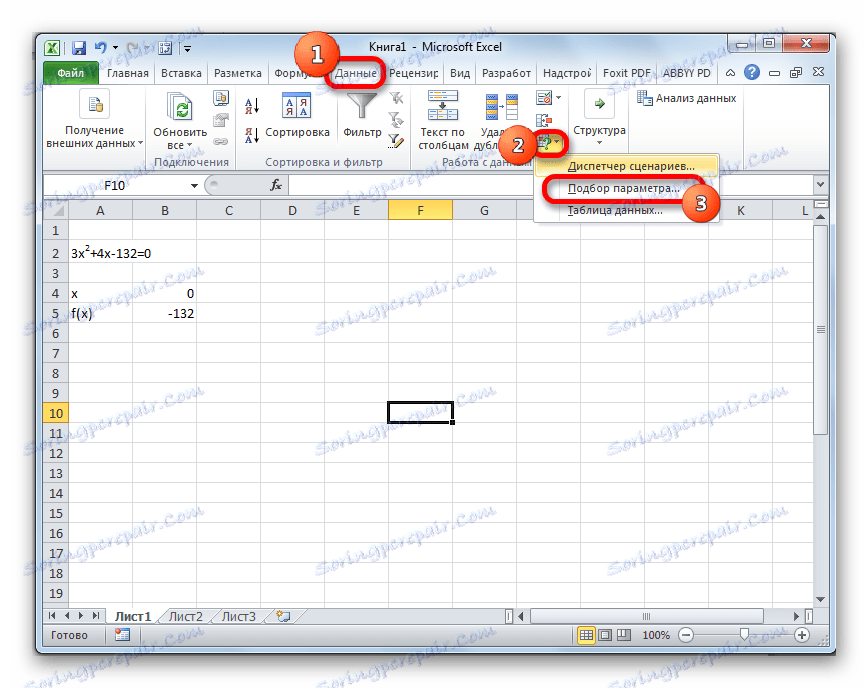
2. Prejdite na kartu "Dáta" . Kliknite na tlačidlo "Analýza toho, čo ak" . Toto tlačidlo je umiestnené na páse v krabici s nástrojmi "Práca s údajmi" . Zobrazí sa rozbaľovací zoznam. Vyberte položku "Výber parametrov ..." .
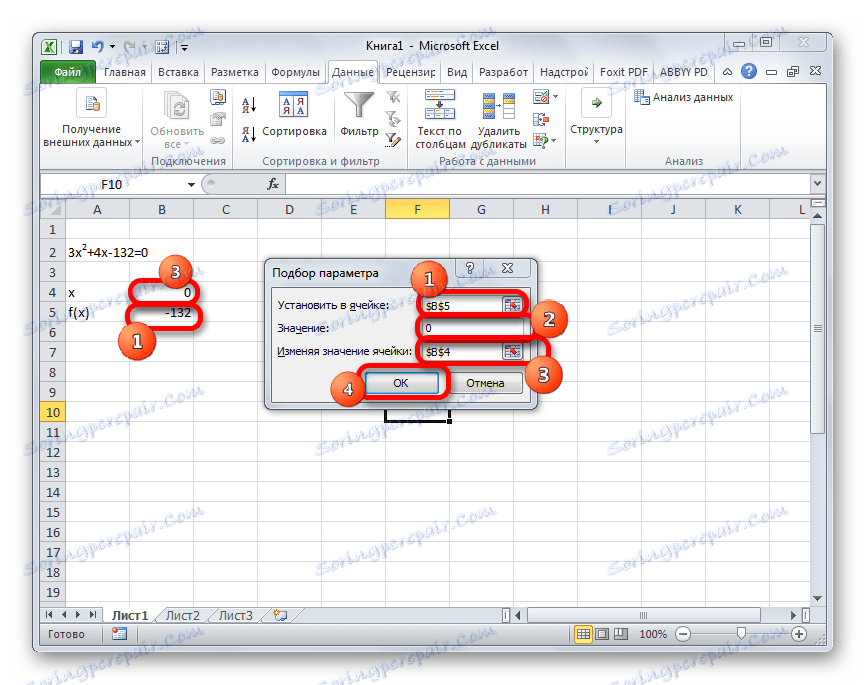
3. Otvorí sa okno pre výber parametrov. Ako môžete vidieť, pozostáva z troch polí. V poli "Nastaviť v bunke" určujeme adresu bunky, v ktorej je nájdený vzorec f (x) , ktorý sme vypočítali o niečo skôr. V poli "Hodnota" zadajte číslo "0" . V poli "Zmena hodnôt" uvádzame adresu bunky, v ktorej je umiestnená hodnota x , ktorú sme predtým urobili pre 0 . Po dokončení týchto krokov kliknite na tlačidlo "OK" .
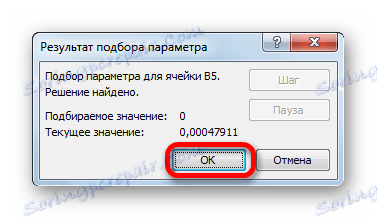
4. Potom vykoná výpočet Excel výber parametra. Toto sa zobrazí v informačnom okne, ktoré sa objavilo. V ňom kliknite na tlačidlo "OK" .
5. Výsledok výpočtu koreňa rovnice bude v bunke, ktorú sme priradili do poľa "Zmeny hodnôt" . V našom prípade, ako vidíme, x bude rovno 6 .

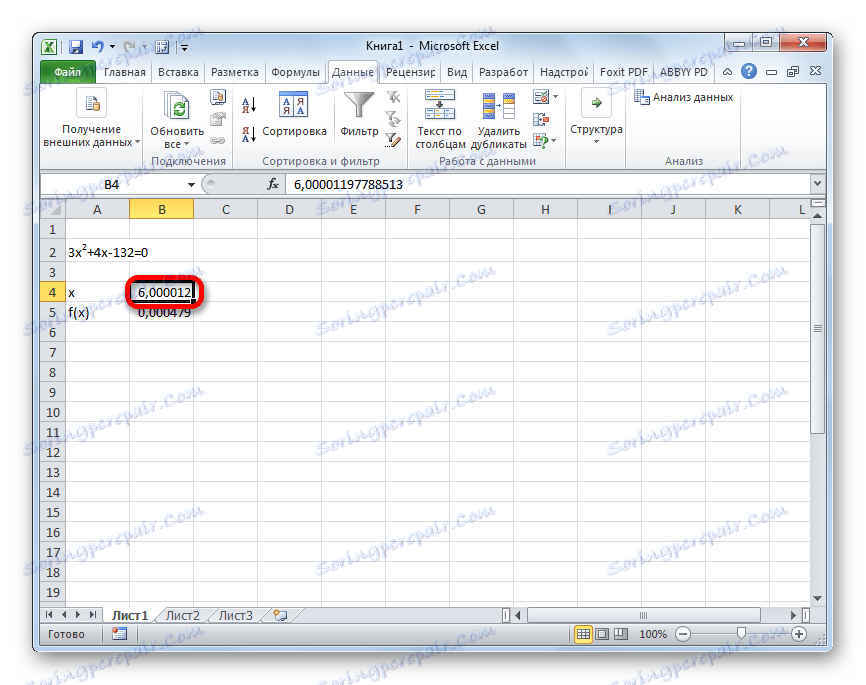
Tento výsledok možno skontrolovať aj nahradením tejto hodnoty riešiteľným výrazom namiesto hodnoty x .

Lekcia: Výber parametrov v programe Excel

Metóda 3: Cramerova metóda

Teraz sa pokúsime vyriešiť systém rovníc pomocou metódy Cramer. Vykonajte napríklad ten istý systém, ktorý bol použitý v režime 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


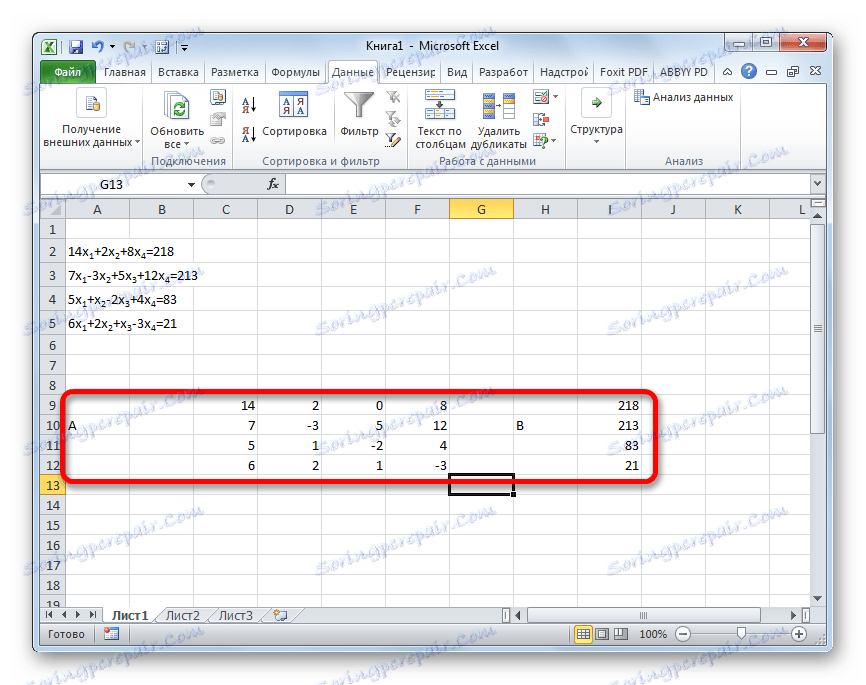
1. Rovnako ako v prvej metóde, zostavujeme maticu A z koeficientov rovníc a tabuľky B z hodnôt, ktoré stoja za znamienkom "rovnaké" .
2. Potom urobíme ešte štyri tabuľky. Každá z nich je kópiou matice A , iba pre tieto kópie sa jeden stĺpec nahrádza jednou tabuľkou B. Prvá tabuľka má prvý stĺpec, druhá tabuľka obsahuje druhý stĺpec atď.
3. Teraz musíme vypočítať determinanty pre všetky tieto tabuľky. Systém rovníc bude mať riešenia len vtedy, ak majú všetky determinanty hodnotu odlišnú od nuly. Na výpočet tejto hodnoty v programe Excel sa opäť nachádza samostatná funkcia - MOPRED . Syntax tohto operátora je:

   =МОПРЕД(массив)

   Tak ako v prípade funkcie MBD , jediným argumentom je odkaz na spracovanú tabuľku.

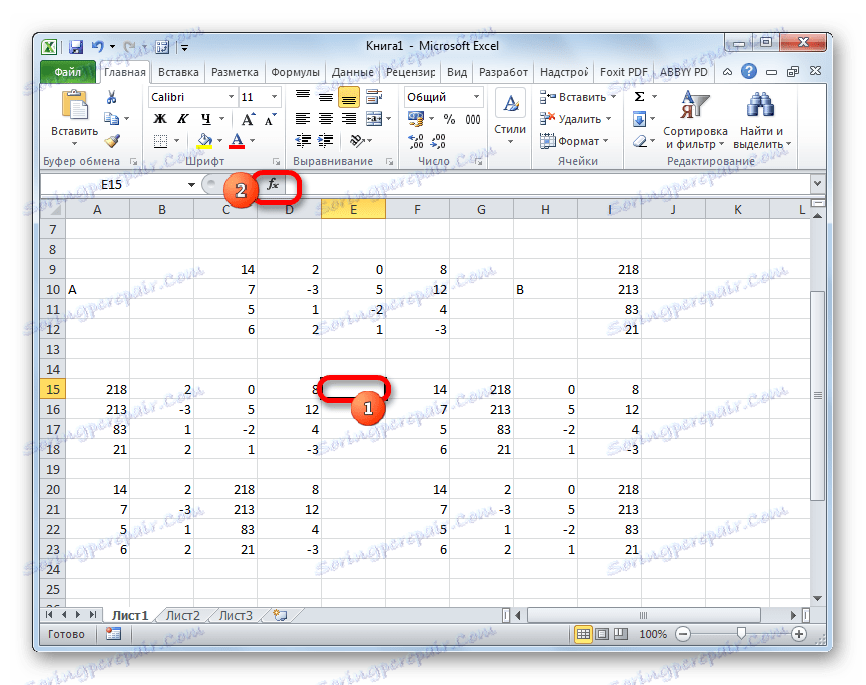
   Vyberte bunku, v ktorej sa bude zobrazovať determinant prvej matice. Potom kliknite na tlačidlo "Vložiť funkciu" , ktoré je známe z predchádzajúcich metód.

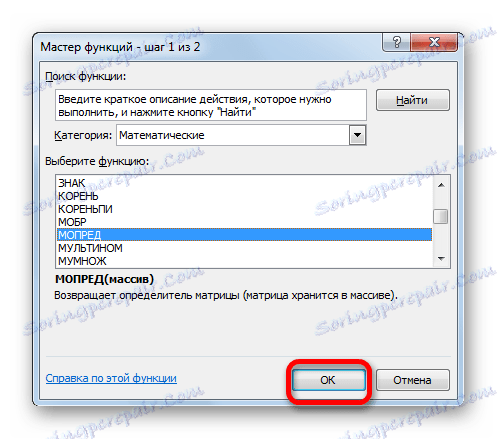
4. Okno Sprievodcovia je aktivované. Prejdeme do kategórie "Matematické" a v zozname prevádzkovateľov vyberieme tam názov "MOPRED" . Potom kliknite na tlačidlo "OK" .
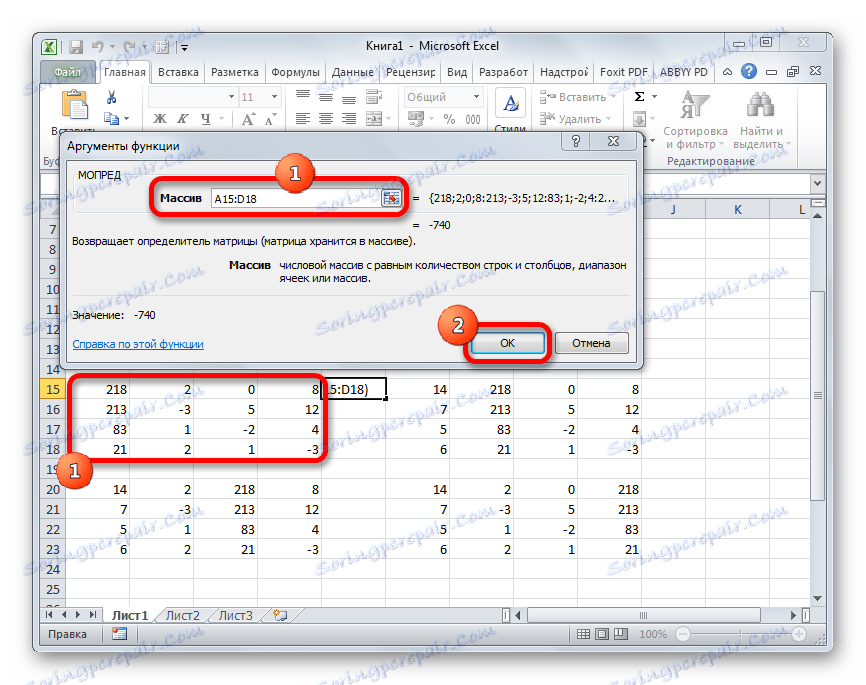
5. Otvorí sa okno s argumentmi funkcie MOPED . Ako vidíte, má len jedno pole - "Array" . V tomto poli zadáme adresu prvej transformovanej matice. Za týmto účelom nastavte kurzor v poli a potom vyberte rozsah matice. Potom kliknite na tlačidlo "OK" . Táto funkcia vygeneruje výsledok do jednej bunky, nie do poľa, takže pre výpočet nemusíte stláčať klávesy Ctrl + Shift + Enter .
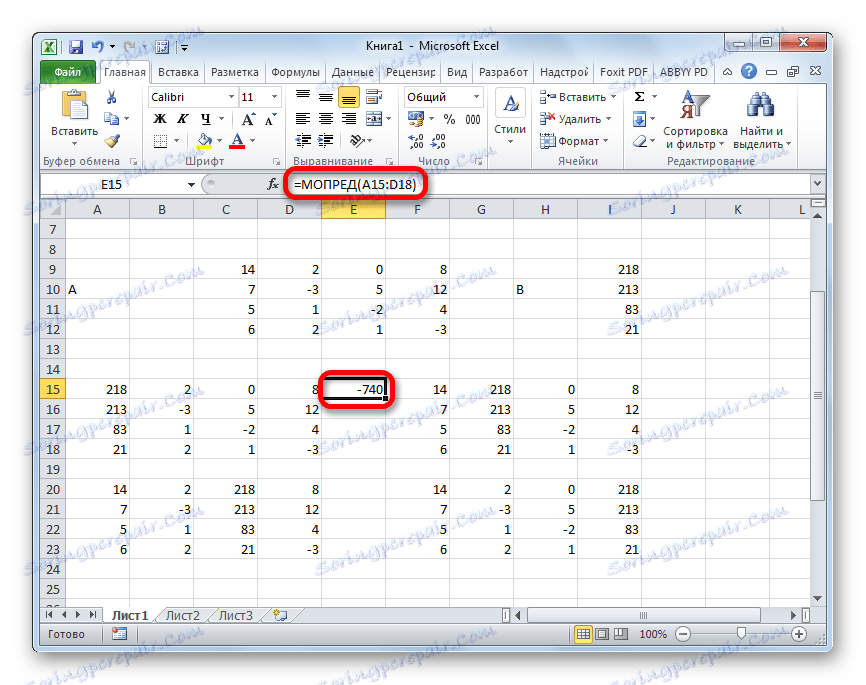
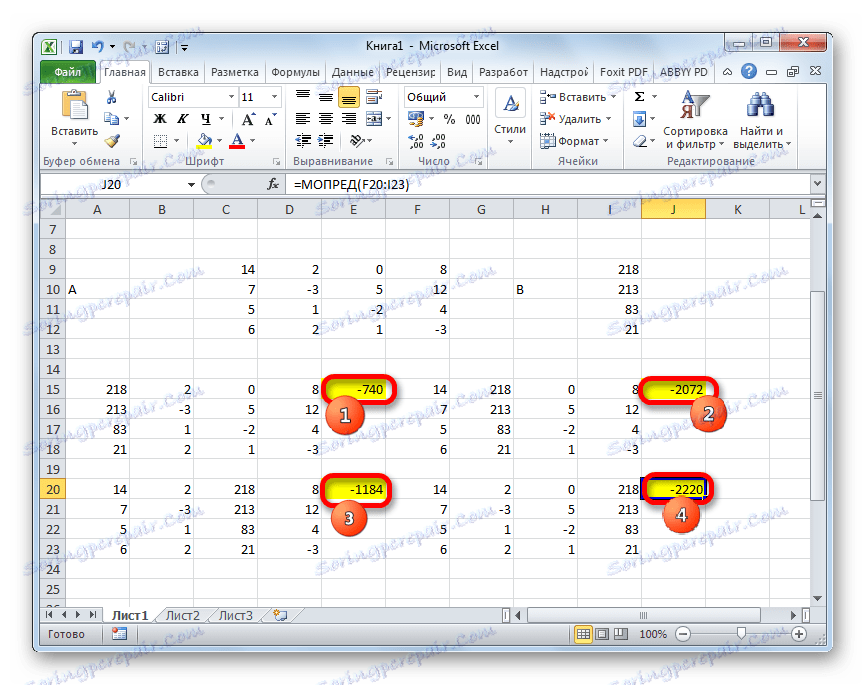
6. Funkcia vypočíta výsledok a vyvedie ho do predvolenej bunky. Ako vidíte, v našom prípade je determinantom -740 , to znamená, že nie je rovný nule, čo je pre nás vhodné.
7. Podobne vypočítame aj determinanty zostávajúcich troch tabuliek.
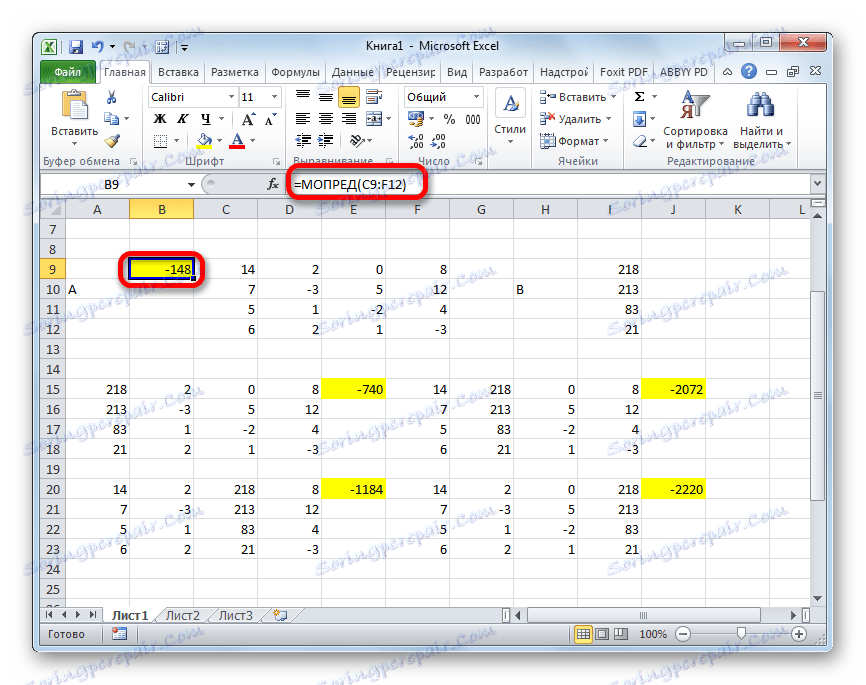
8. V záverečnej fáze vypočítame determinant primárnej matrice. Postup je rovnaký pre ten istý algoritmus. Ako môžete vidieť, determinant primárnej tabuľky sa tiež líši od nuly, a preto je matrica považovaná za nerozvinutú, to znamená, že systém rovníc má riešenia.
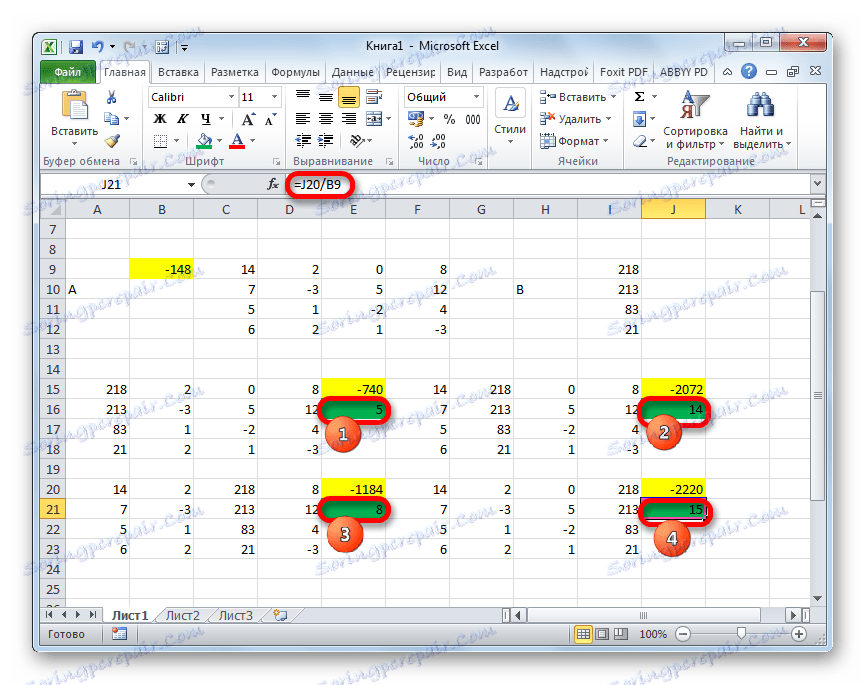
9. Teraz je čas nájsť korene rovnice. Koreň rovnice sa bude rovnať pomeru determinantu zodpovedajúcej transformovanej matrice k determinantu primárnej tabuľky. Takže po rozdelení všetkých štyroch determinantov transformovaných matíc jeden po druhom -148 , ktorý je determinantom pôvodnej tabuľky, získame štyri korene. Ako vidíte, sú rovnaké ako hodnoty 5 , 14 , 8 a 15 . Preto sa presne zhodujú s koreňmi, ktoré sme našli pomocou inverznej matice v metóde 1 , čo potvrdzuje správnosť riešenia systému rovníc.

Metóda 4: Gaussova metóda

Riešenie systému rovníc je možné vykonať aj pomocou metódy Gauss. Napríklad, vezmime jednoduchší systém rovníc troch neznámych:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


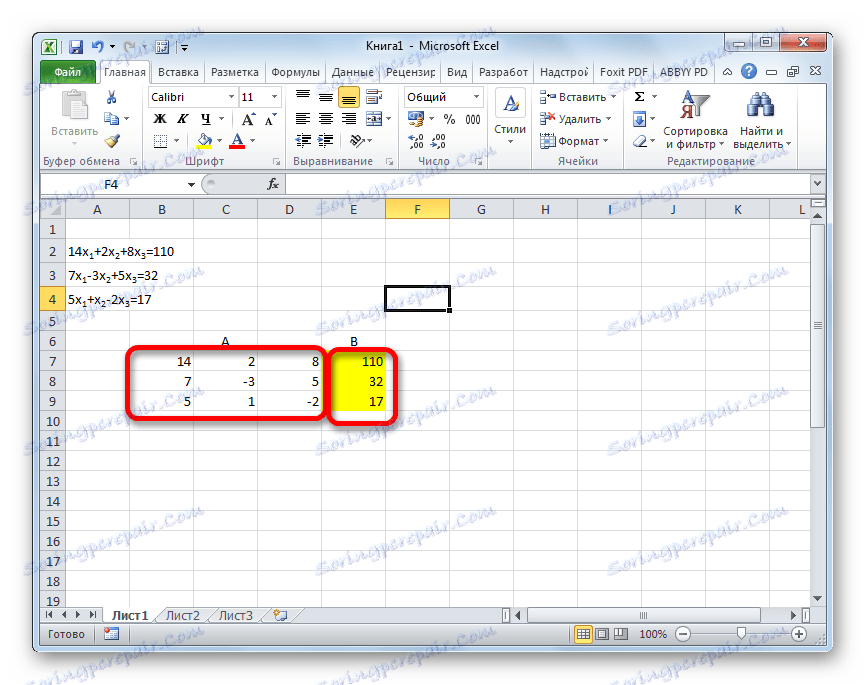
1. Znova postupne zaznamenávame koeficienty v tabuľke A a voľné termíny nachádzajúce sa za znamienkom "sa rovná" v tabuľke B. Tentokrát však budeme zblížiť obe tabuľky, pretože to bude nevyhnutné pre prácu v budúcnosti. Dôležitou podmienkou je, že v prvej bunke matrice A sa hodnota líši od nuly. V opačnom prípade by ste mali usporiadať riadky na miestach.
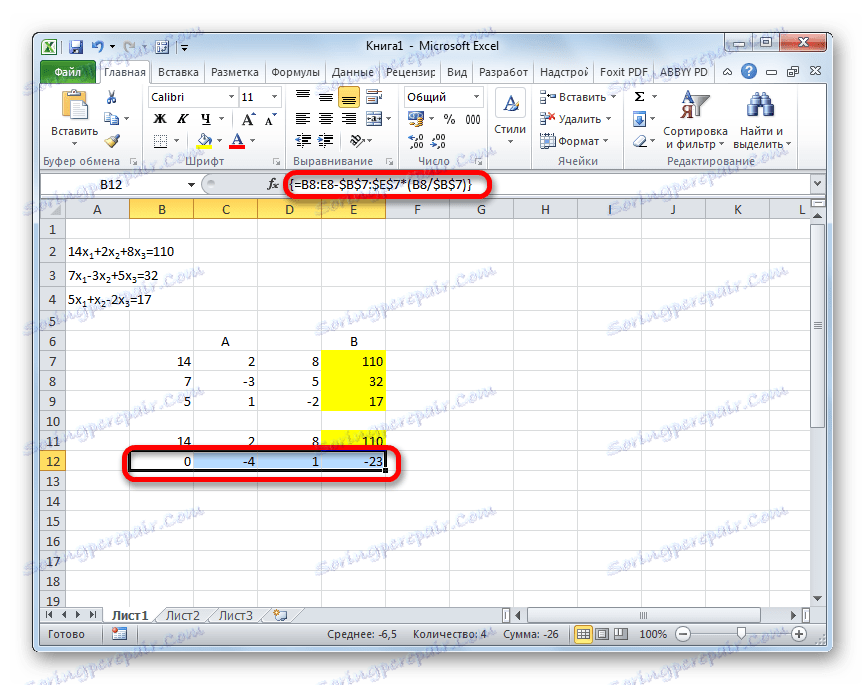
2. Skopírujte prvý riadok dvoch pripojených matic v riadku dole (pre jasnosť môžete preskočiť jeden riadok). V prvej bunke, ktorá je umiestnená v riadku ešte nižšie ako predchádzajúca, zadáme nasledujúci vzorec:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Ak usporiadate matrice inak, potom budú adresy buniek vzorca mať pre vás inú hodnotu, ale môžete ich vypočítať porovnaním s vzorcami a obrázkami, ktoré sú tu uvedené.

   Po zadaní vzorca zadajte celý riadok buniek a stlačte klávesy Ctrl + Shift + Enter . Vzorec poľa bude použitý na riadok a bude vyplnený hodnotami. Preto sme odpočítali od druhého riadku prvý, vynásobený pomerom prvých koeficientov prvých dvoch výrazov systému.

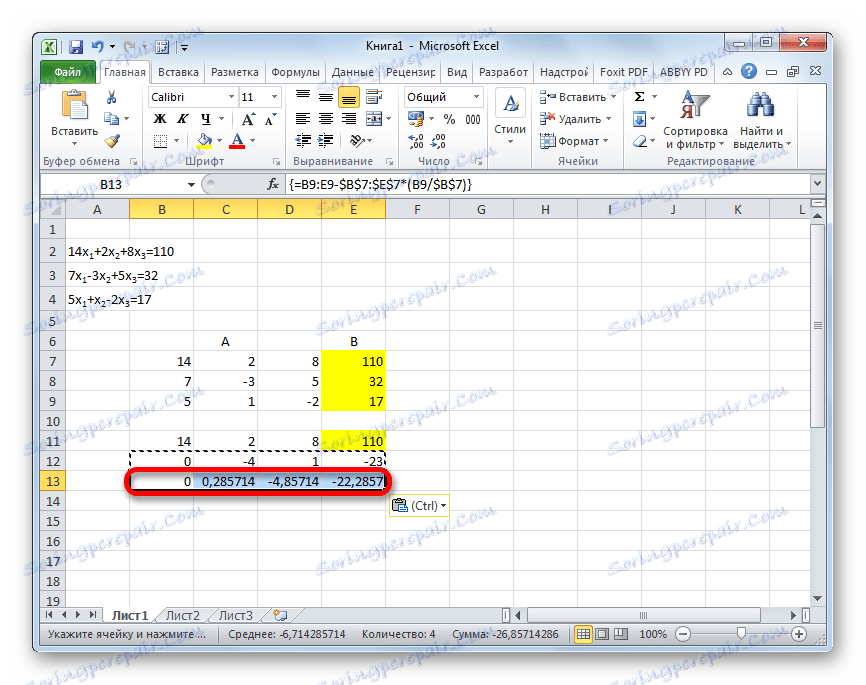
3. Potom výsledný riadok skopírujte a vložte ho do riadku uvedeného nižšie.
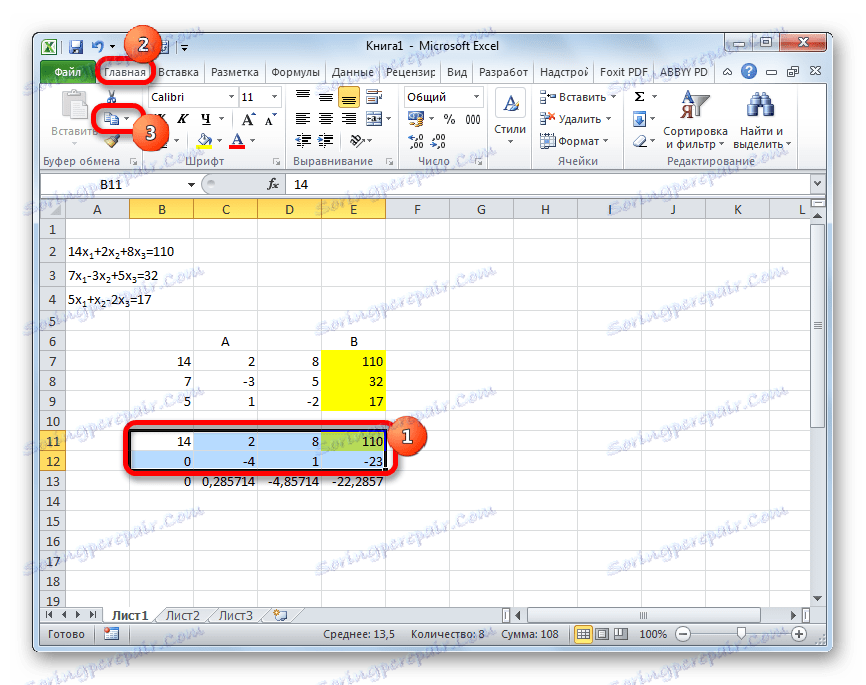
4. Vyberte prvé dva riadky za chýbajúcou čiarou. Kliknite na tlačidlo "Kopírovať" , ktoré sa nachádza na páse na karte "Domov" .
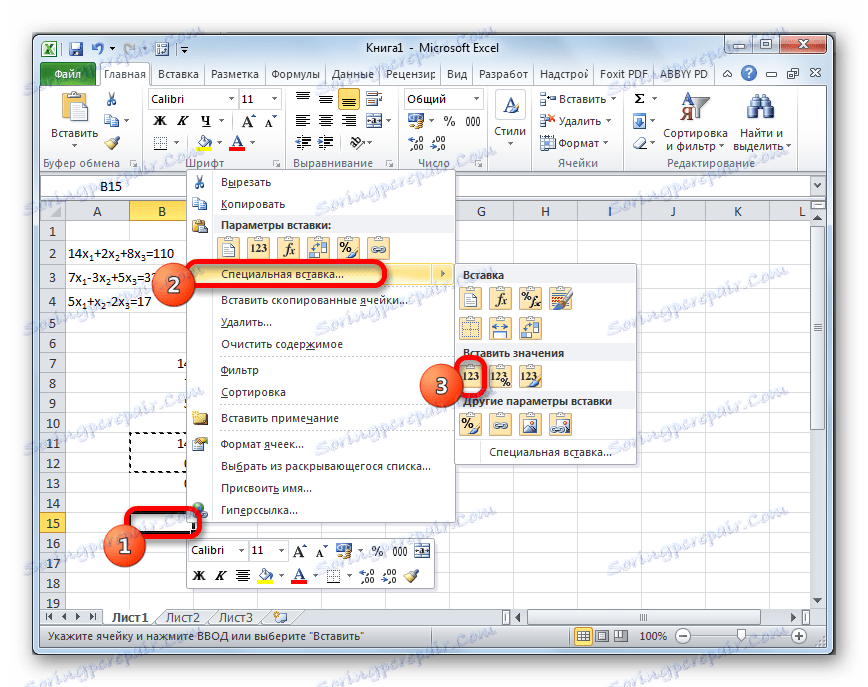
5. Preskočíme linku po poslednom zázname na hárku. Vyberte prvú bunku v ďalšom riadku. Kliknite pravým tlačidlom myši. V otvorenom kontextovom menu umiestňujeme kurzor nad položku "Zvláštna prilepka" . V dodatočnom zozname, ktorý sa spustí, vyberte položku "Hodnoty" .
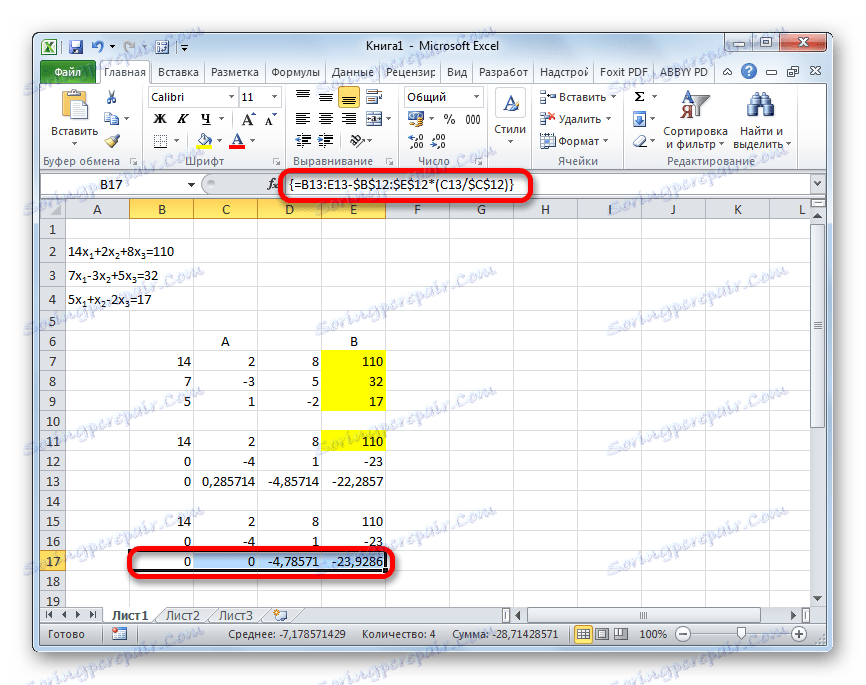
6. V nasledujúcom riadku zadajte vzorec poľa. Odčíta druhý riadok od tretieho riadku predchádzajúcej skupiny údajov vynásobenej pomerom druhého koeficientu tretieho a druhého riadku. V našom prípade bude vzorec mať nasledujúcu formu:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   Po zadaní vzorca si vyberte celú sériu a aplikujte klávesovú skratku Ctrl + Shift + Enter .

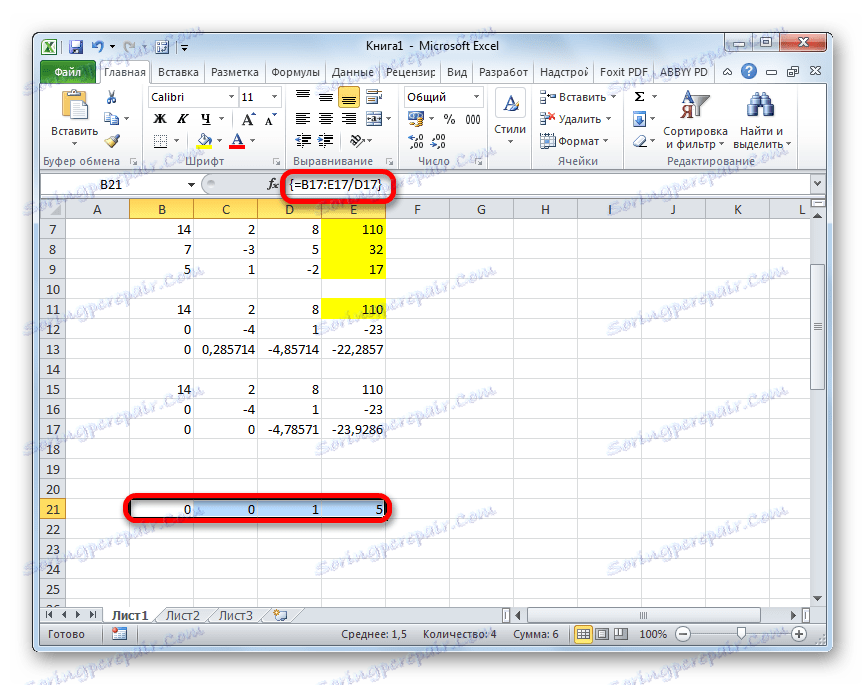
7. Teraz je potrebné vykonať spätný chod pomocou metódy Gauss. Z posledného záznamu preskočíme tri riadky. V štvrtom riadku zadáme vzorec poľa:

   =B17:E17/D17

   Preto rozdelíme posledný riadok, ktorý sme vypočítali podľa svojho tretieho koeficientu. Po zadaní vzorca si zvoľte celý riadok a stlačte klávesy Ctrl + Shift + Enter .

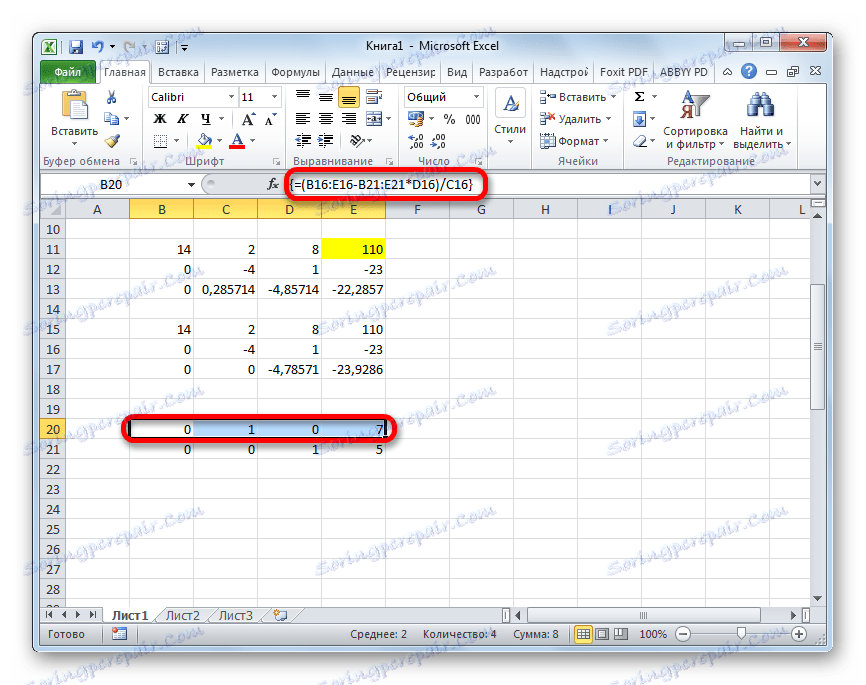
8. Stúpame na čiaru smerom hore a do nej vstupujeme nasledujúci vzorec poľa:

   =(B16:E16-B21:E21*D16)/C16

   Stlačením zvyčajnej kombinácie klávesov použijeme vzorec poľa.

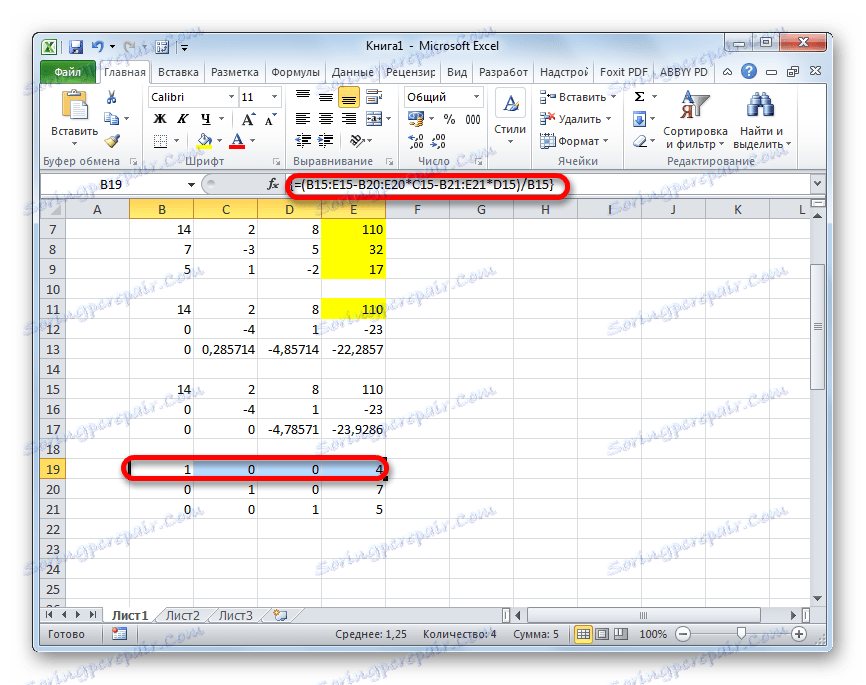
9. Zvyšujeme ešte jednu čiaru. V ňom zadáme vzorec poľa nasledujúceho formulára:

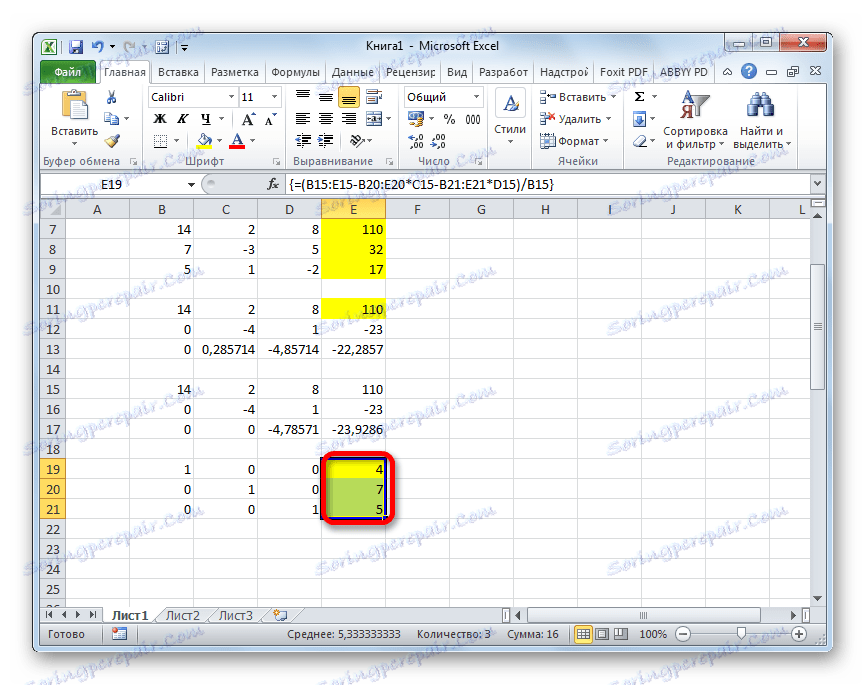
   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Znova vyberte celý riadok a aplikujte kombináciu klávesov Ctrl + Shift + Enter .

10. Teraz sa pozrite na čísla, ktoré boli získané v poslednom stĺpci posledného bloku riadkov, ktoré sme vypočítali predtým. Práve tieto čísla ( 4 , 7 a 5 ) budú korene daného systému rovníc. Môžete to skontrolovať tak, že ich namiesto X1 , X2 a X3 nahradíte vo výrazoch.

Ako vidíte, v systéme Excel môže byť systém rovníc vyriešený mnohými spôsobmi, z ktorých každý má svoje vlastné výhody a nevýhody. Všetky tieto metódy však možno podmienene rozdeliť na dve veľké skupiny: matice a pomocou nástroja na výber parametrov. V niektorých prípadoch nie sú vždy vhodné maticové metódy na riešenie problému. Konkrétne, keď je determinant matrice nula. V iných prípadoch sa užívateľ môže slobodne rozhodnúť, akú možnosť považuje za výhodnejšiu pre seba.

• ← Vytvorenie paraboly v programe Microsoft Excel
• Vytvorenie tlačidla v programe Microsoft Excel →