vynikať

Použitie analýzy klastrov v programe Microsoft Excel

Jedným z nástrojov na riešenie ekonomických problémov je analýza klastrov. Pri jeho použití sú zhluky a iné objekty v rade údajov rozdelené do skupín. Táto metóda môže byť použitá v programe Excel. Pozrime sa, ako sa to v praxi vykonáva.

Použitie analýzy klastrov

Pomocou klastrovej analýzy je možné vzorkovať na základe toho, čo sa skúma. Jeho hlavnou úlohou je rozdeliť multidimenzionálne pole do homogénnych skupín. Ako kritérium zoskupenia sa podľa daného parametra použije korelačný koeficient pár alebo euklidovská vzdialenosť medzi objektmi. Najbližšie k sebe navzájom sú zoskupené.

Hoci sa tento typ analýzy používa najčastejšie v ekonomike, môže sa použiť aj v biológii (klasifikácia zvierat), v psychológii, medicíne av mnohých ďalších oblastiach ľudskej činnosti. Klastrová analýza môže byť použitá pomocou štandardného súboru nástrojov programu Excel na tento účel.

Príklad použitia

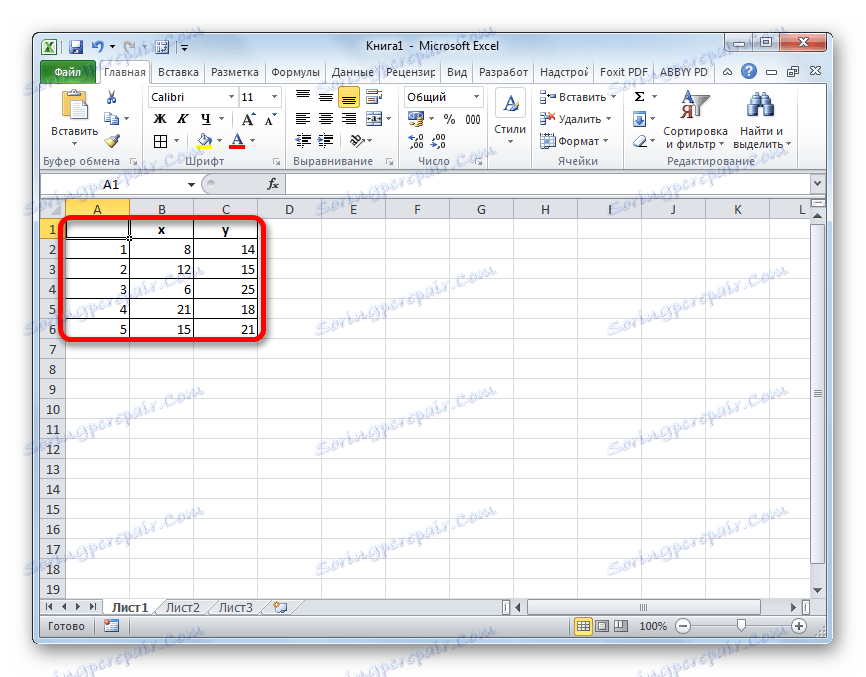
Máme päť objektov, ktoré sú charakterizované dvoma sledovanými parametrami - x a y .

  1. Na tieto hodnoty sa aplikuje vzorec euklidovskej vzdialenosti, ktorý sa vypočíta zo šablóny:

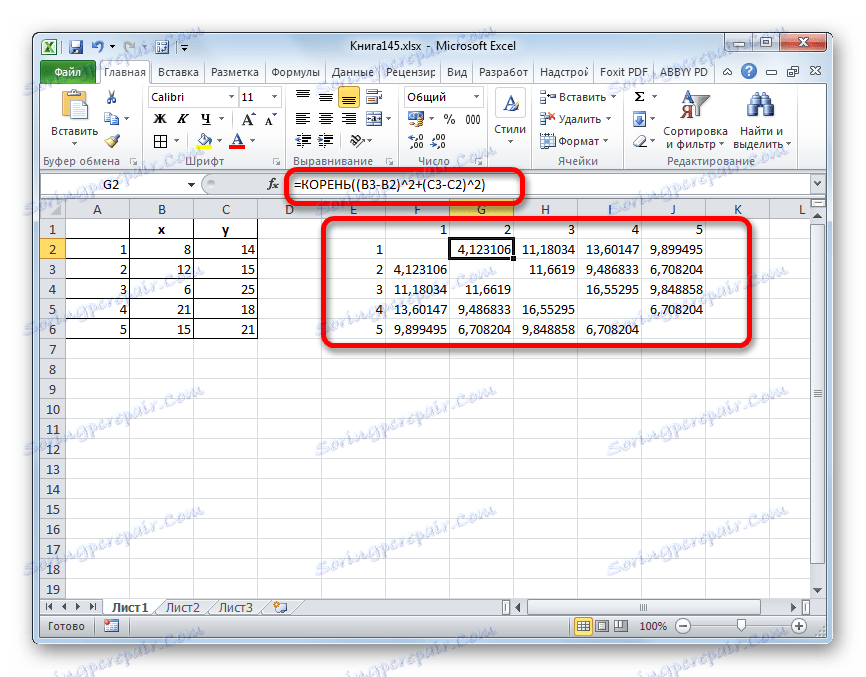
    =КОРЕНЬ((x2-x1)^2+(y2-y1)^2)

    2. Naučené objekty v programe Microsoft Excel

  2. Táto hodnota sa vypočítava medzi každým z piatich objektov. Výsledky výpočtu sú umiestnené v matici vzdialeností.

    3. Matica vzdialenosti v programe Microsoft Excel

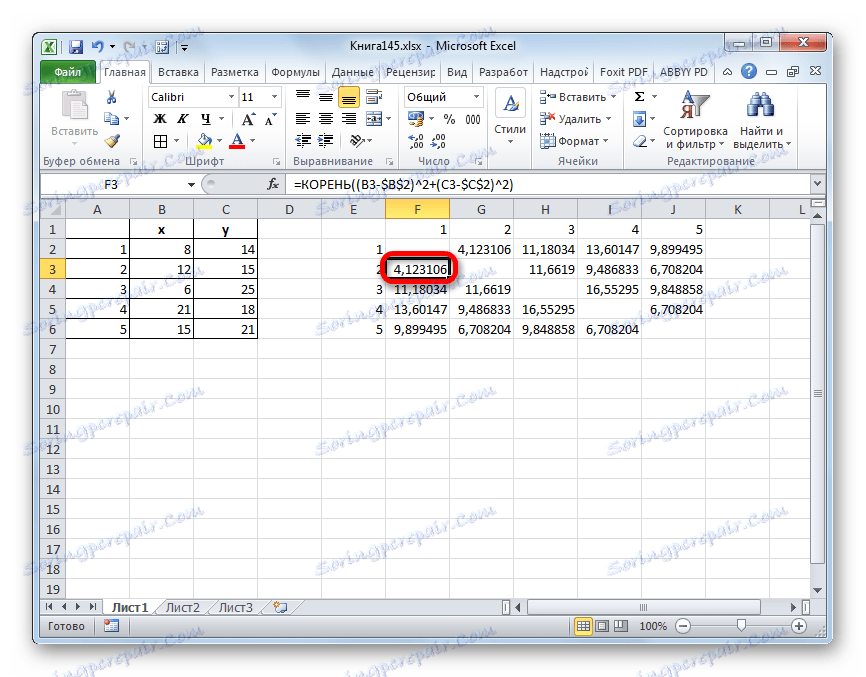
  3. Pozeráme sa, medzi ktorými hodnotami je najmenšia vzdialenosť. V našom príklade sú to objekty 1 a 2 . Vzdialenosť medzi nimi je 4.123106, čo je menej ako medzi inými prvkami danej populácie.

    4. V aplikácii Microsoft Excel je vzdialenosť medzi objektmi minimálna

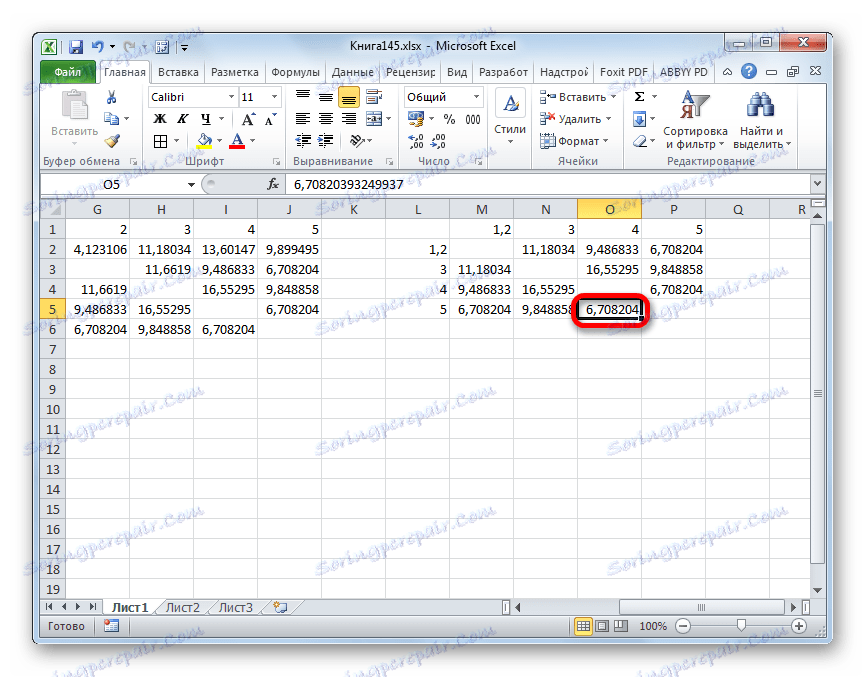
  4. Tieto údaje spájame do skupiny a tvoria novú maticu, v ktorej hodnoty 1,2 sú samostatným prvkom. Pri zostavovaní matice ponecháme najmenšie hodnoty z predchádzajúcej tabuľky pre kombinovaný prvok. Opäť sa pozrieme, medzi ktorými prvkami je vzdialenosť minimálna. Tentokrát to je 4 a 5 , a tiež objekt 5 a skupina objektov 1,2 . Vzdialenosť je 6,708204.

    5. V druhej matici v programe Microsoft Excel je vzdialenosť medzi objektmi minimálna

  5. Pridané prvky pridáme do všeobecného klastra. Vytvárame novú maticu na rovnakom princípe ako v predchádzajúcom období. To znamená, že hľadáme najnižšie hodnoty. Preto vidíme, že náš súbor údajov možno rozdeliť na dva klastre. V prvom klastri sú najbližšie prvky 1 , 2 , 4 , 5 . V druhom klastri je v našom prípade zastúpený iba jeden prvok - 3 . Je pomerne ďaleko od iných objektov. Vzdialenosť medzi klastrami je 9,84.

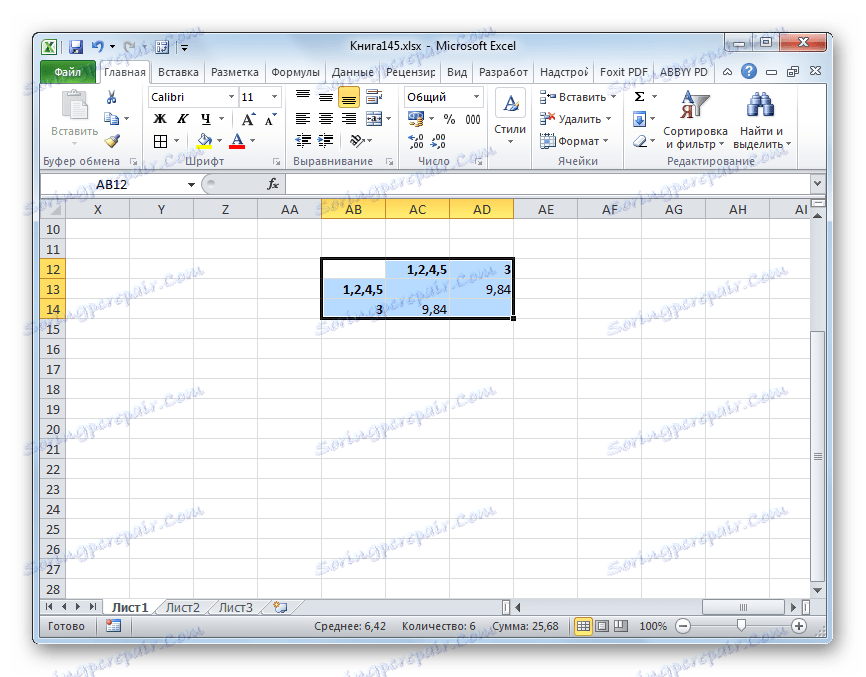
Celková hodnota v programe Microsoft Excel

Tým sa uzatvára postup rozdelenia zbierky do skupín.

Ako vidíte, aj keď sa vo všeobecnosti analýza klastrov môže zdať komplikovaný postup, nie je tak ťažké pochopiť nuansy tejto metódy. Hlavnou vecou je pochopiť základný model zoskupenia.